前言

最近夜梦在学习有限差分，在此记录一下。

如果没学习过这方面的知识，夜梦推荐先看第四章 有限差分方法-1.基本概念了解有限差分的基本概念，然后从一维$(x,t)$问题开始学习有限差分的相关知识。

简单来说，有限差分旨在解决一个核心问题：如何在离散的网格点上，通过已知位置已知时间的物理量（$V^k_n$与其相关网格点）递推求解未来时刻（如$V^{k+1}_n$）的量。

---

在学习了有限差分之后，为了能够较好的借助matlab模拟出介质中波场的传播，设置合理的边界条件是必须的。夜梦推荐先从分裂场PML开始尝试，比较好理解。强烈推荐阅读：弹性波和声波的时域仿真方法研究，这篇文章中，作者对声波与弹性波的PML方法都做了详细介绍，通俗易懂。

---

在学习完成有限差分、PML边界条件等内容后，就可以使用matlab进行简单模拟。代码在最后，前面先放代码的解析。

1. 物理模型与基本参数

假设均匀介质，二维无限空间，波源（震源）为ricker子波。

f0   = 5;          % Ricker 主频 Hz
dt   = 1e-3;       % 时间步长 s
dx   = 3;          % 空间步长 m
dz   = 3;
v    = 500;        % 波速 m/s
rho  = 1000;       % 密度 kg/m^3
kappa = rho*v^2;   % 体积模量

这里的物理量：

• 波速 $v = 500\ \text{m/s}$
• 密度 $\rho = 1000\ \text{kg/m}^3$
• 体积模量 $\kappa = \rho v^2$

即$\kappa = \rho v^2$

声学的一阶形式方程是（二维）：

$\begin{cases} \rho \dfrac{\partial v_x}{\partial t} = – \dfrac{\partial p}{\partial x}, \\[6pt] \rho \dfrac{\partial v_z}{\partial t} = – \dfrac{\partial p}{\partial z}, \\[6pt] \dfrac{1}{\kappa} \dfrac{\partial p}{\partial t} = – \left( \dfrac{\partial v_x}{\partial x} + \dfrac{\partial v_z}{\partial z} \right). \end{cases}$

2. CFL 稳定性条件

为了保证有限差分的稳定，必须满足CFL稳定性条件。

CFL = v*dt/min(dx,dz);
fprintf('CFL = %.4f', CFL);

$\text{CFL} = \frac{v,\Delta t}{\min(\Delta x, \Delta z)}$

对二维声学波动方程，显式FDM通常要求：

$\text{CFL} \lesssim \frac{1}{\sqrt{2}}$

3. 网格与震源位置

nx   = 201; 
nz   = 201;
x    = (0:nx-1)*dx;
z    = (0:nz-1)*dz;

ix0  = floor(nx/2)+1;
iz0  = floor(nz/2)+1;
x0   = x(ix0);
z0   = z(iz0);

网格大小：$201 \times 201$ 点

震源放在网格中心 $(x_0, z_0)$

4. Ricker 子波公式

t  = (0:nt-1)*dt;
t0 = 1.5/f0;  % 主峰时间
src_t = (1 - 2*(pi*f0*(t-t0)).^2) .* exp(-(pi*f0*(t-t0)).^2);

Ricker 子波标准形式：

$s(t) = \left[1 – 2(\pi f_0 (t – t_0))^2 \right] \exp\left(-(\pi f_0 (t – t_0))^2\right)$

$f_0 = 5\ \text{Hz}$：主频；

$(t_0 = 1.5/f_0)$：主峰出现的时间。

ricker子波常用于地震勘探。

5. 交错网格变量

vx = zeros(nz, nx+1);   % x方向速度，交错半格
vz = zeros(nz+1, nx);   % z方向速度，交错半格
px = zeros(nz, nx);     % 分裂压力场
pz = zeros(nz, nx);
p  = zeros(nz, nx);     % 总压力场

$v_x(i,j+\tfrac12)$：定义在单元边界的 x 方向速度

$v_z(i+\tfrac12,j)$：定义在单元边界的 z 方向速度

$p(i,j)$：压力（这里拆成 $(p_x, p_z)$ 用于 PML）

交错网格的优点是数值色散和稳定性相对更好。

6. PML 阻尼系数的构造

6.1 阻尼剖面最大值公式

npml = 30;                  % PML 层厚度
Rcoef = 1e-6;               % 目标反射系数
m = 2;                      % PML 阶数
...
Lx = npml * dx;
sigma_max_x = -(m+1)*v*log(Rcoef) / (2*Lx);
...
Lz = npml * dz;
sigma_max_z = -(m+1)*v*log(Rcoef) / (2*Lz);

PML 阻尼的最大值取自常用公式：

$\sigma_{\max} = -\frac{(m+1)v}{2L} \ln(R_\text{coef})$

其中：

$L$ 是 PML 层厚度（$L_x = \text{npml}\cdot\Delta x$ 或 $L_z = \text{npml}\cdot\Delta z$）

$R_\text{coef}$ 是希望在边界的反射系数，比如 $10^{-6}$

$m$ 是多项式阶数（这里 $m=2$）

6.2 位置相关的阻尼分布

以 x 方向为例，代码做的是：

在左 PML：

$x_\text{Norm} = \frac{\text{npml} – i_x + 1}{\text{npml}} \in (0,1]$

在右 PML：

$x_\text{Norm} = \frac{i_x – (n_x-\text{npml})}{\text{npml}}$

阻尼：

$\sigma_x(i_z, i_x) = \sigma_{\max,x} , x_\text{Norm}^m$

z 方向类似：

$\sigma_z(i_z, i_x) = \sigma_{\max,z} , z_\text{Norm}^m$

接着插值到交错网格上的 $\sigma X_{vx}, \sigma Z_{vz}$，用于速度更新：

sigmaX_vx(:, 2:end-1) = (sigmaX(:, 1:end-1) + sigmaX(:, 2:end)) / 2;
...
sigmaZ_vz(2:end-1, :) = (sigmaZ(1:end-1, :) + sigmaZ(2:end, :)) / 2;

7. 核心 FDM + PML 更新公式

主循环：

for it = 1:nt
    % 1) 更新 vx
    dpdx = (p(:, 2:end) - p(:, 1:end-1)) / dx;
    vx(:, 2:end-1) = vx(:, 2:end-1) .* (1 - dt*sigmaX_vx(:, 2:end-1)) ...
                     - dt*(1/rho) .* dpdx;
    
    % 2) 更新 vz
    dpdz = (p(2:end, :) - p(1:end-1, :)) / dz;
    vz(2:end-1, :) = vz(2:end-1, :) .* (1 - dt*sigmaZ_vz(2:end-1, :)) ...
                     - dt*(1/rho) .* dpdz;

    % 3) 更新 px, pz
    dvx_dx = (vx(:, 2:end) - vx(:, 1:end-1)) / dx;
    px = px .* (1 - dt*sigmaX) - kappa*dt .* dvx_dx;
    
    dvz_dz = (vz(2:end, :) - vz(1:end-1, :)) / dz;
    pz = pz .* (1 - dt*sigmaZ) - kappa*dt .* dvz_dz;

    % 4) 加源
    px(iz0, ix0) = px(iz0, ix0) + src_t(it);

    % 5) 合成总压力
    p = px + pz;
    ...
end

7.1 连续方程的 PML 形式

在 PML 中，压力被分裂成两部分：

$p = p_x + p_z$

并引入阻尼 $\sigma_x, \sigma_z$，方程变成：

$\begin{cases} \rho \dfrac{\partial v_x}{\partial t} + \rho \sigma_x^{(vx)} v_x = -\dfrac{\partial p}{\partial x}, \\[8pt] \rho \dfrac{\partial v_z}{\partial t} + \rho \sigma_z^{(vz)} v_z = -\dfrac{\partial p}{\partial z}, \\[8pt] \dfrac{\partial p_x}{\partial t} + \sigma_x p_x = -\kappa \dfrac{\partial v_x}{\partial x}, \\[8pt] \dfrac{\partial p_z}{\partial t} + \sigma_z p_z = -\kappa \dfrac{\partial v_z}{\partial z}. \end{cases}$

7.2 时间离散（显式）

以 $v_x$ 为例：

$\frac{v_x^{n+1} – v_x^n}{\Delta t} + \sigma_x^{(vx)} v_x^n = -\frac{1}{\rho}\left(\frac{\partial p}{\partial x}\right)^n$

整理：

$v_x^{n+1} = v_x^n \left(1 – \Delta t\ \sigma_x^{(vx)} \right)-\Delta t \frac{1}{\rho} \left(\frac{\partial p}{\partial x}\right)^n$

对应代码：

vx = vx .* (1 - dt*sigmaX_vx) - dt*(1/rho) .* dpdx;

$v_z$也是一样形式，只是用 $\sigma_z^{(vz)}$ 与 $\partial p / \partial z$。

7.3 空间差分（中心差分）

例如：

$\left(\frac{\partial p}{\partial x}\right){i,j} \approx \frac{p{i,j+1} – p_{i,j}}{\Delta x}$

对应代码：

dpdx = (p(:, 2:end) - p(:, 1:end-1)) / dx;

同理：

$\left(\frac{\partial p}{\partial z}\right){i,j} \approx \frac{p{i+1,j} – p_{i,j}}{\Delta z}$

对应代码：

dpdz = (p(2:end, :) - p(1:end-1, :)) / dz;

7.4 分裂压力的离散更新

以 $p_x$ 为例：

$\frac{p_x^{n+1} – p_x^n}{\Delta t} + \sigma_x p_x^n = -\kappa\left(\frac{\partial v_x}{\partial x}\right)^n$

$p_x^{n+1} = p_x^n(1 – \Delta t\sigma_x)-\kappa\Delta t \left(\frac{\partial v_x}{\partial x}\right)^n$

代码：

dvx_dx = (vx(:, 2:end) - vx(:, 1:end-1)) / dx;
px = px .* (1 - dt*sigmaX) - kappa*dt .* dvx_dx;

$p_z$ 同理，用 $\partial v_z/\partial z$ 和 $\sigma_z$。

7.5 加入震源与总压力

震源加在 $p_x$ 上：

px(iz0, ix0) = px(iz0, ix0) + src_t(it);

即在点 $(x_0,z_0)$ 让：

$p_x^{n+1}(x_0,z_0) \leftarrow p_x^{n+1}(x_0,z_0) + s(t_n)$

最后总压力：
$p = p_x + p_z$

说实话，wordpress上面数学公式的展示字体有点小，看的费眼睛。

8. GIF展示

有限差分法：

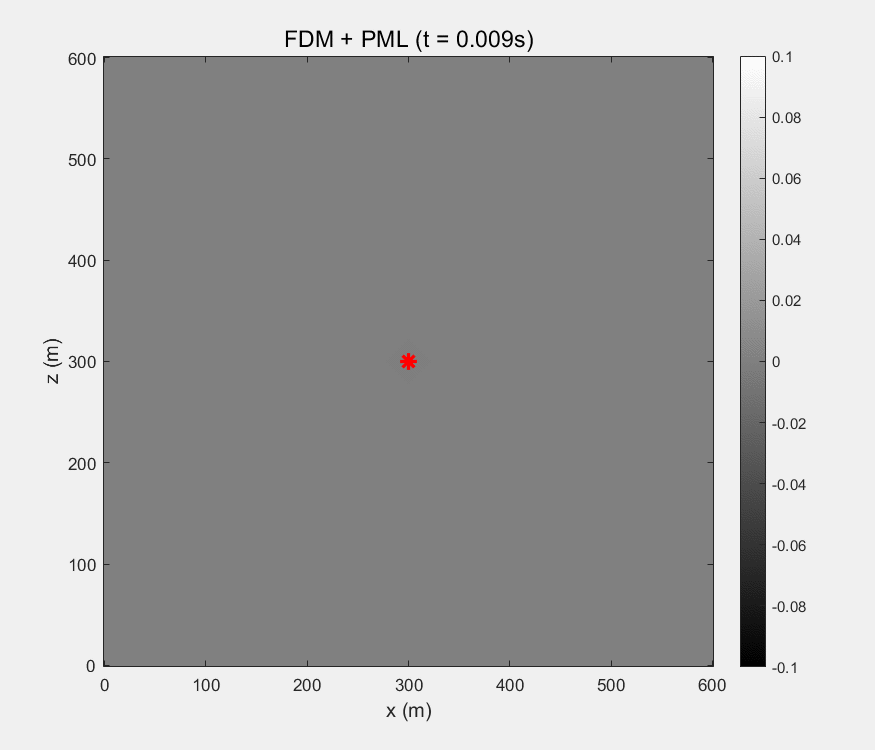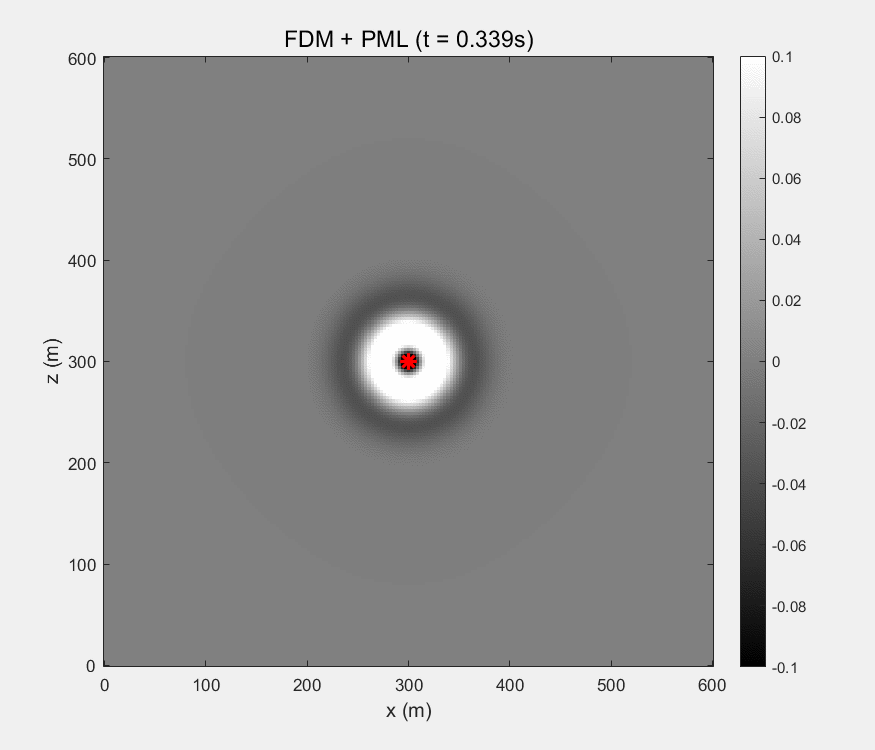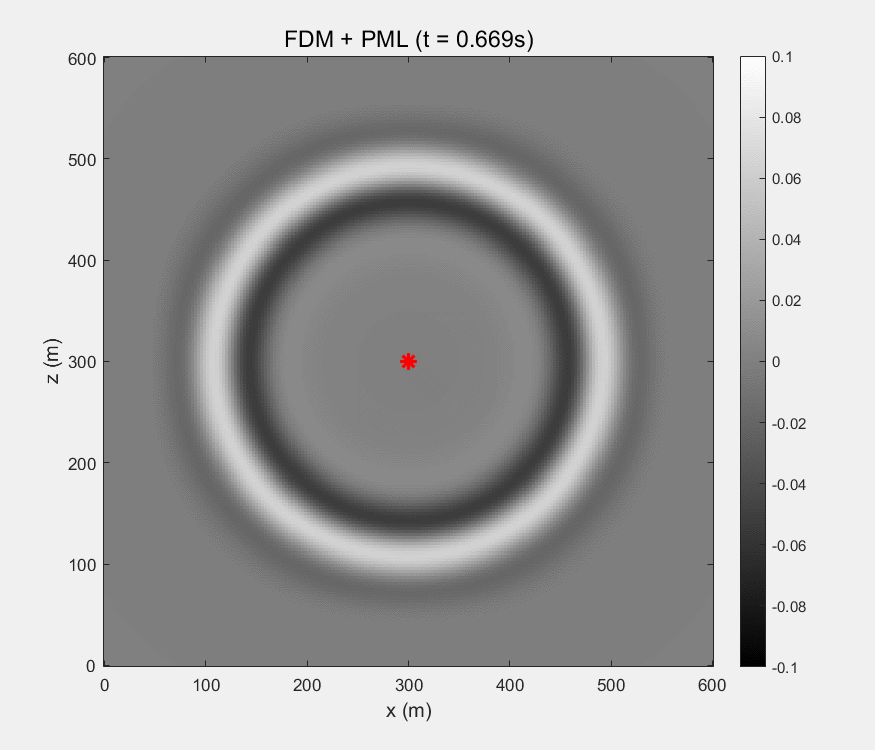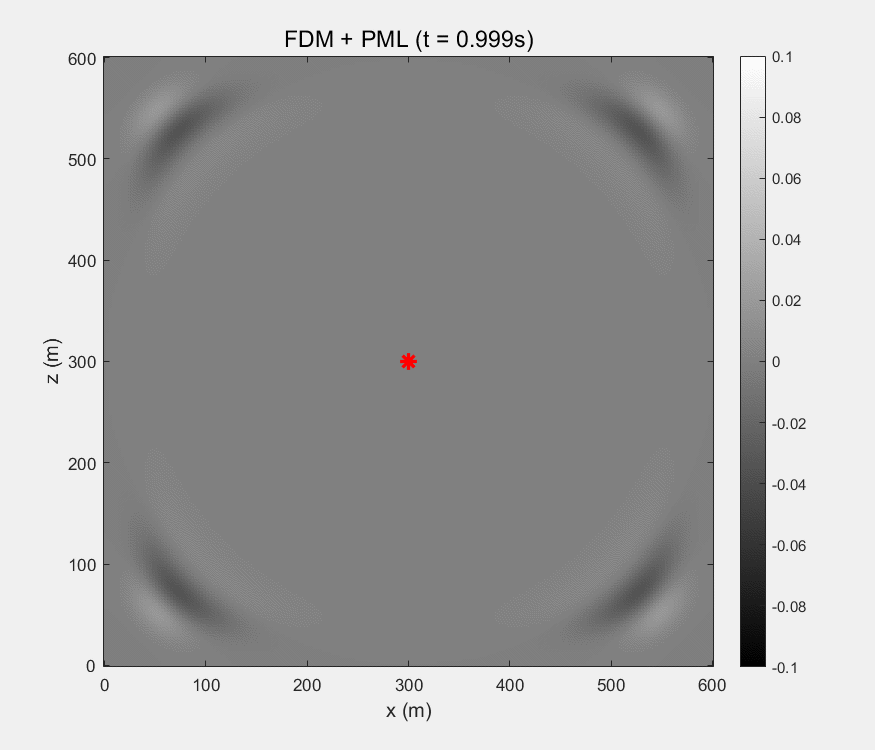
9. matlab代码

以下是matlab代码，仅供参考：

clear; clc; close all;

%% ========= 基本参数 =========
f0   = 5;          % Ricker 主频 Hz
dt   = 1e-3;       % 时间步长 s (缩小以满足稳定性)
dx   = 3;          % 空间步长 m
dz   = 3;
v    = 500;        % 波速 m/s
rho  = 1000;       % 密度 kg/m^3
kappa = rho*v^2;   % 体积模量

% CFL 稳定性检查
CFL = v*dt/min(dx,dz);
fprintf('CFL = %.4f', CFL);

nt   = 1000;        % 总时间步数
nplot = 10;         % 每隔几步画一次图

nx   = 201; 
nz   = 201;
x    = (0:nx-1)*dx;
z    = (0:nz-1)*dz;

% 源在网格中心
ix0  = floor(nx/2)+1;
iz0  = floor(nz/2)+1;
x0   = x(ix0);
z0   = z(iz0);

%% ========= Ricker 子波 =========
t  = (0:nt-1)*dt;
t0 = 1.5/f0;  % 主峰时间
src_t = (1 - 2*(pi*f0*(t-t0)).^2) .* exp(-(pi*f0*(t-t0)).^2);

%% ========= 交错网格变量初始化 =========
% vx(i,j+1/2), vz(i+1/2,j), p(i,j)
vx = zeros(nz, nx+1);   % x方向速度，交错半格
vz = zeros(nz+1, nx);   % z方向速度，交错半格
px = zeros(nz, nx);     % 分裂压力场
pz = zeros(nz, nx);
p  = zeros(nz, nx);     % 总压力场

%% ========= 构造 PML 阻尼系数 =========
npml = 30;                  % PML 层厚度
Rcoef = 1e-6;               % 目标反射系数
m = 2;                      % PML 阶数

% 初始化阻尼系数（定义在压力网格点）
sigmaX = zeros(nz, nx);
sigmaZ = zeros(nz, nx);

% 同时需要交错网格上的阻尼系数
sigmaX_vx = zeros(nz, nx+1);  % 用于vx更新
sigmaZ_vz = zeros(nz+1, nx);  % 用于vz更新

% x 方向最大阻尼
Lx = npml * dx;
sigma_max_x = -(m+1)*v*log(Rcoef) / (2*Lx);

% z 方向最大阻尼
Lz = npml * dz;
sigma_max_z = -(m+1)*v*log(Rcoef) / (2*Lz);

% 左右 PML （sigmaX，压力点）
for ix = 1:nx
    if ix <= npml
        xNorm = (npml - ix + 1)/npml;
        sx = sigma_max_x * xNorm^m;
    elseif ix >= nx-npml+1
        xNorm = (ix - (nx-npml))/npml;
        sx = sigma_max_x * xNorm^m;
    else
        sx = 0;
    end
    sigmaX(:, ix) = sx;
end

% 上下 PML （sigmaZ，压力点）
for iz = 1:nz
    if iz <= npml
        zNorm = (npml - iz + 1)/npml;
        sz = sigma_max_z * zNorm^m;
    elseif iz >= nz-npml+1
        zNorm = (iz - (nz-npml))/npml;
        sz = sigma_max_z * zNorm^m;
    else
        sz = 0;
    end
    sigmaZ(iz, :) = sz;
end

% 插值到交错网格
sigmaX_vx(:, 2:end-1) = (sigmaX(:, 1:end-1) + sigmaX(:, 2:end)) / 2;
sigmaX_vx(:, 1) = sigmaX(:, 1);
sigmaX_vx(:, end) = sigmaX(:, end);

sigmaZ_vz(2:end-1, :) = (sigmaZ(1:end-1, :) + sigmaZ(2:end, :)) / 2;
sigmaZ_vz(1, :) = sigmaZ(1, :);
sigmaZ_vz(end, :) = sigmaZ(end, :);

%% ========= GIF ：FDM + PML 波场 =========
gifname1 = 'fdm_pml_wavefield_bw.gif';

figure('Position',[100 100 700 600])
iframe = 0;

for it = 1:nt
    % ---- 1) 更新速度（交错网格差分）----
    % vx: 使用 dp/dx
    dpdx = (p(:, 2:end) - p(:, 1:end-1)) / dx;
    vx(:, 2:end-1) = vx(:, 2:end-1) .* (1 - dt*sigmaX_vx(:, 2:end-1)) ...
                     - dt*(1/rho) .* dpdx;
    
    % vz: 使用 dp/dz
    dpdz = (p(2:end, :) - p(1:end-1, :)) / dz;
    vz(2:end-1, :) = vz(2:end-1, :) .* (1 - dt*sigmaZ_vz(2:end-1, :)) ...
                     - dt*(1/rho) .* dpdz;

    % ---- 2) 更新分裂压力场 ----
    % dvx/dx
    dvx_dx = (vx(:, 2:end) - vx(:, 1:end-1)) / dx;
    px = px .* (1 - dt*sigmaX) - kappa*dt .* dvx_dx;
    
    % dvz/dz
    dvz_dz = (vz(2:end, :) - vz(1:end-1, :)) / dz;
    pz = pz .* (1 - dt*sigmaZ) - kappa*dt .* dvz_dz;

    % ---- 3) 加入震源 ----
    px(iz0, ix0) = px(iz0, ix0) + src_t(it);

    % ---- 4) 合成总压力场 ----
    p = px + pz;

    % ---- 5) 画图（每隔 nplot 步）----
    if mod(it, nplot) == 0
        iframe = iframe + 1;
        
        imagesc(x, z, p);
        axis equal tight;
        set(gca,'YDir','normal');
        colormap(gray);  % 黑白配色
        clim([-1e-1 1e-1]);
        title(sprintf('FDM + PML (t = %.3fs)', t(it)), 'FontSize', 14);
        xlabel('x (m)', 'FontSize', 12); 
        ylabel('z (m)', 'FontSize', 12);
        colorbar;
        
        % 标记震源位置
        hold on;
        plot(x0, z0, 'r*', 'MarkerSize', 10, 'LineWidth', 2);
        hold off;
        
        drawnow;

        frame = getframe(gcf);
        im = frame2im(frame);
        [A,map] = rgb2ind(im,256);
        if iframe == 1
            imwrite(A,map,gifname1,'gif','LoopCount',inf,'DelayTime',0.05);
        else
            imwrite(A,map,gifname1,'gif','WriteMode','append','DelayTime',0.05);
        end
    end
end